決定係数の導出をおさらい
備忘的にメモ。
平方和の分解
回帰直線を用いるとき、応答変数(目的変数)の変動の大きさを表す平方和
は、回帰による平方和
と残差平方和
の和
の形に分解できる。
観測値の平方和の式を変形すると
となる。
ここで、右辺第3項は予測値と残差の偏差積和を表すが、予測値と残差の相関係数が0であるため、この項は0。
また、第1項と第2項を入れ替え、
と観測値の平方和
は2つの平方和の和の形に分解できる。
ここで、右辺の第1項は回帰による平方和 (RはRegressionを指す)、第2項は残差平方和
と呼ぶ。
決定係数
上記、平方和の分解のうち、の平方和の中の回帰による平方和の割合
を決定係数、又は寄与率と呼ぶ。
理解しやすいように以下にまとめると、
- :応答変数yの変動の大きさを表す
- :回帰直線によって説明される部分
- :回帰直線によって説明されない部分
となる。
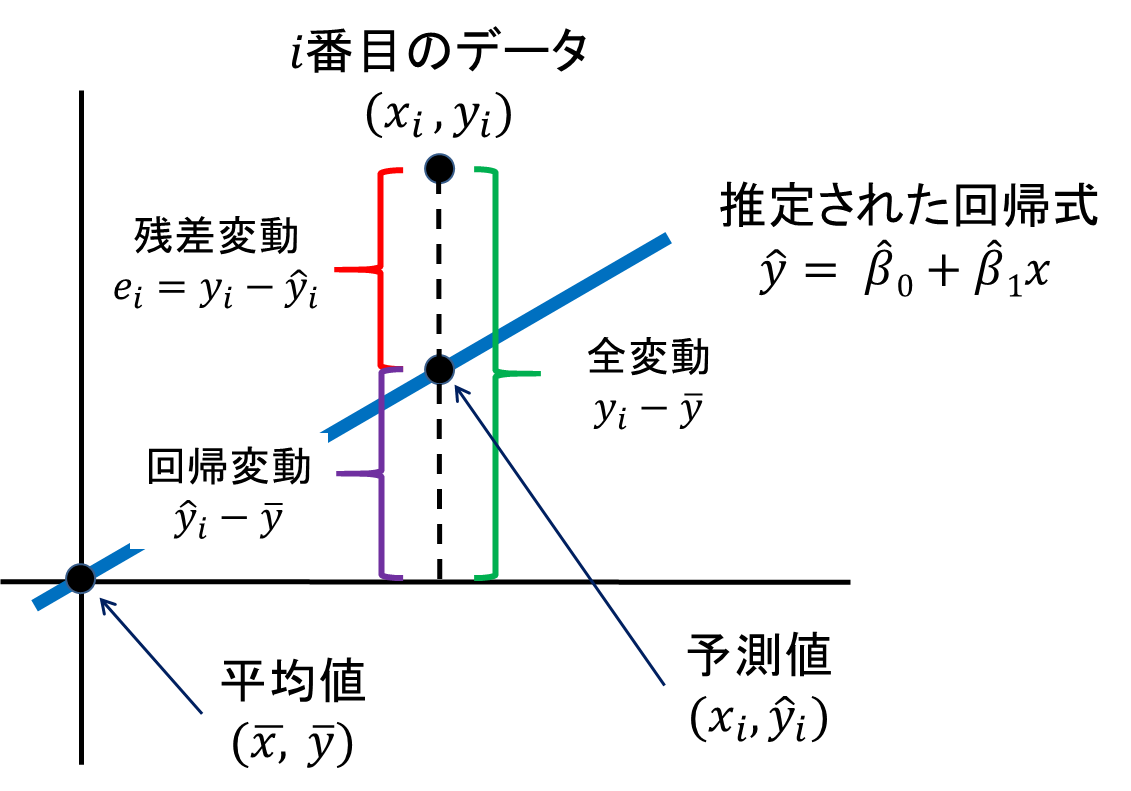
下図は統計Webより引用ですが、直感的に理解する上で非常に参考になります。このサイト自体解説も分かりやすいです。